During the past week shocking news have stormed through the world of Theoretical Computer Science. A researcher from HP Labs, Vinay Deolalikar claimed that he had a proof that P NP.

The paper is available here. But so far it seems that it will not stand. Several researchers pointed out critical defects in the proof that Deolalikar proposed. It is especially interesting to follow the discussion in Dick Liptons blog (In 5 posts so far: 1 2 3 4 5). Or in Wikipedia for the short version. Its amazing to see how many of the worlds most brilliant mathematicians worked so fast to analyze Deolalikars proof, including Terence Tao, and Timothy Gowers. The fatal blow to the attempted proof seems to be in a letter from Neil Immerman. There are plenty of references about the proposed proof and the refutations in this Wiki.

Now for anybody that is not an expert in complexity theory (myself included), here is a short explanation of what this is all about and why it matters: P and NP are two classes of algorithms. Colloquially, algorithms in P are those for which the amount of time that it takes to execute with an input of size n is a polynomial of n. For example, finding the maximum in a list of n elements takes approximately n steps because we just need to go through all n elements and keep track of the maximum. Problems for which the best possible algorithm is in P are in general solvable in reasonable time, because even for large values of the input the time that it takes to run the algorithm is not too big.

Algorithms in NP are those for which, if we have a proposed solution, we can check if it actually solves the problem in polynomial time. For example, given a set of integers {7, 3, 2, 5, 8} of size 5 we can check if a subset like {3, 2, 5} adds up to zero in less than 5 steps. We simply need to add the numbers. However finding a solution in general takes a much bigger number of steps. One way to solve it is to analyze all subsets, and for each one, check if its a solution. But the number of subsets grows exponentially with n, hence the difficulty.

Obviously all algorithms in P are also in NP, because if we can find the solution in polynomial time then we can verify the solution in polynomial time (for example by finding it again). The complex question is whether P is equal to NP or not.

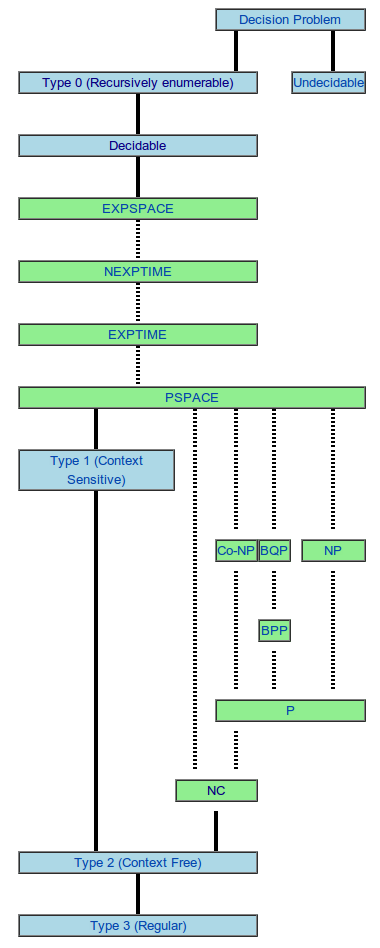
These two classes of algorithms are especially interesting for their practical applications but there are not the only classes by any means. The following diagram shows some of the most important ones. The classes at the bottom are contained in the classes on top.

And there are many more. The Complexity Zoo lists 489 complexity classes.

Now that we have seen what the problem is about, why does it matter? I am going to talk about two important real world consequences of a possible proof of P=NP. You can find many more here if you are interested.

The first application is in mathematical research. As Stephen Cook says, we can verify a proof of a theorem in polynomial time so if P=NP then we would be able to create a proof in polynomial time. This would allow us to build automatic theorem provers that basically do scientific research for us 24/7, continuously discovering new knowledge. Its obvious the tremendous repercussions that this would have in the world.

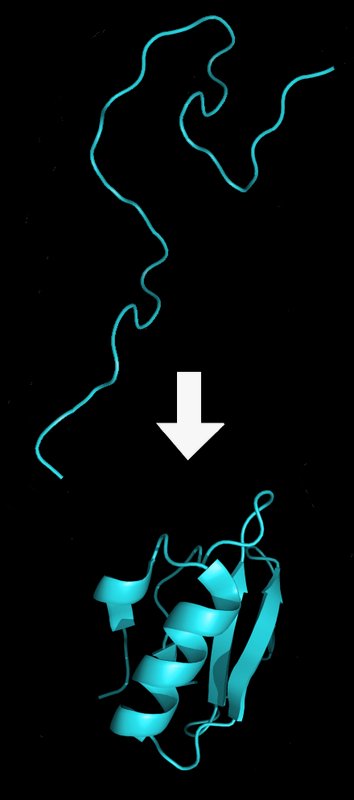
The second example is in biology. It is known that the HP protein folding model is in NP. This model basically simplifies the way that amino acids fold in space to form proteins, the essential actors in all cells. If we had an algorithm in P to solve this problem we could possibly design substances that have specific 3D shapes and properties, instead of simply finding them. For example some vaccines work because the 3D shape of a protein in the vaccine fits the 3D shape of a protein in the pathogen. Who knows how many illnesses we could cure with that technology.